CMU 15-110 Spring 2019: Principles of Computing
Homework 6 (Due Tuesday 9-Apr at 8pm)

---

Except for the TA-led session on recursion, this hw is entirely solo. See the syllabus for details.

---

To start, download this file: hw6.py

---

1. TA-Led Sessions on Recursion [40 pts, not autograded]
   Your recitation TA's will organize 1-hour TA-led sessions in which you will review recursion exercises. To get the hw6 points for this, you need to show up on time (even a few minutes early), stay the whole time, and be very actively involved the whole time. This should be easy to do, since recursion is fascinating! Have fun!


2. inAllSets(L) [15 pts, autograded]
   Write the function inAllSets(L) that takes a list of sets, and returns a set of all the values that occur in ALL the sets in the list. If L is empty, return the empty set. For example:

       assert(inAllSets([{1,2,3}, {0,2,4}, {5,8,1}]) == set())
       assert(inAllSets([{1,2,3}, {0,2,4}, {5,8,2}]) == {2})
       assert(inAllSets([{1,2,3}, {1,2,4}, {2,8,1}]) == {1,2})

   Hint: you may find the & (set intersection) operator very useful here:

       s = { 1, 2, 3 }
       t = { 0, 2, 4 }
       print(s & t)  # prints {2}, the intersection of sets s and t

   Another hint: { } is not an empty set, but rather an empty dictionary!


3. makeCityStateMaps(cityList) [30 pts, autograded]
   Write the function makeCityStateMaps(cityList) that takes a list cityList of pairs of values -- (city, state), like ('Chicago', 'Illinois') -- and returns a list of 3 separate dictionaries [ statesToCities, citiesToStates, and cityCounts ]. The first, statesToCities, maps each unique state name to a set of the cities that are in that state. The second, citiesToStates, does the opposite, and maps each unique city name to a set of the states that that city name appears in. Finally, the last, cityCounts, maps each unique city name to a count of the total number of states it occurs in. For example:

       cityList = [ ('Erie', 'PA'), ('York', 'PA'), ('Erie', 'WV') ]
       assert(makeCityStateMaps(cityList) ==
               [
                   # statesToCities
                   { 'PA' : { 'Erie', 'York' },
                     'WV' : { 'Erie' }
                   },
                   # citiesToStates
                   { 'Erie' : { 'PA', 'WV' },
                     'York' : { 'PA' }
                   },
                   # cityCounts
                   { 'Erie' : 2,
                     'York' : 1
                   }
               ])

   Hint: this is a nice way to loop over each city,state pair in cityList:

       cityList = [ ('Erie', 'PA'), ('York', 'PA'), ('Erie', 'WV') ]
       for city,state in cityList:
           print(city,state)

   Another hint: use s.add(value) to add a value to a set s.


4. CountingDog Class [15 pts, autograded]
   Write the class CountingDog so that the following test code passes (without hardcoding, so any reasonable edits to the test code still pass):

   def testCountingDogClass():
       print('Testing CountingDog class...', end='')
       d1 = CountingDog('Fred', 5)
       assert(d1.name == 'Fred')
       assert(d1.age == 5)
       assert(d1.count == 0) # counts the number of times the dog speaks
       assert(d1.speak(1) == 'Woof!')
       assert(d1.count == 1)
       assert(d1.speak(3) == 'Woof! Woof! Woof!') # still counts as 1 call to speak
       assert(d1.count == 2) # so the count only went up by 1
   
       d2 = CountingDog('Wilma', 4)
       assert(d2.name == 'Wilma')
       assert(d2.age == 4)
       assert(d2.count == 0)
       assert(d2.speak(4) == 'Woof! Woof! Woof! Woof!')
       assert(d2.count == 1)
       assert(d1.count == 2)
       print('Passed!')



5. Bonus/Optional: Keplers Polygons [up to 3 pts, not autograded]
   Among his lesser-known exploits, the great German mathematician and astronomer Johannes Kepler studied how polygons can tile the plane or portions of the plane. At the bottom of your hw6.py file (importantly, below the #ignore_rest line!), write the function keplerPolygons() that takes no parameters and runs an animation (so you can also include our animation framework in your hw6.py file) that draws one of these Kepler Polygons centered on wherever the user presses the mouse:
   
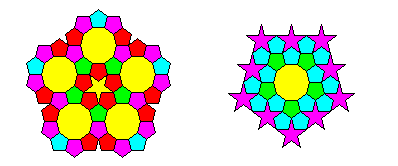
   You can score up to 1 point for each type of Kepler Polygon you draw. If you do more than one, just iterate through them on each subsequent mouse press, so we can just press the mouse a few times to see all of them.
   Hint: it may help to study this example: drawStars.py
   Enjoy!!!

---