CMU 15-112: Fundamentals of Programming and Computer Science
Homework 2 (Due Sat 11-Sep at 8pm ET)
(Optional Early Bird Bonus for Part A is Due Thu 9-Sep at 10pm ET)
Important Notes:
- Read the "Important Notes" at the top of hw1. The same general rules apply to this hw regarding solo, early-bird bonus, sample solution videos, etc.
- This homework is solo. You must not collaborate with anyone (besides current course TA's and faculty) in any way. See the syllabus for more details.
- You will need these starter files:
- For this hw, you may submit up to 7 times to the early-bird submission and up to 7 more times for the main hw submission, but only your last submission counts.
- Do not use strings (except where required in playPig and the bonus problems), string indexing (even in bonus problems), lists, list indexing, or recursion this week.
- Do not hardcode the test cases in your solutions.
Part A [20 pts]
- digitCount(n) [2 pts]
Write the function digitCount(n) that takes a possibly-negative int and returns the number of digits in it. So, digitCount(12323) returns 5, digitCount(0) returns 1, and digitCount(-111) returns 3. One way you could do this would be to return len(str(abs(n))), but you cannot do that, since you may not use strings here! This can be solved with logarithms, but seeing as this is "loops week", you should instead simply repeatedly remove the ones digit until you cannot. - gcd(m, n) [2 pts]
[Note: to receive any credit, you must solve this problem using Euclid's algorithm, and by no other means. In particular, do not just loop through all integers less than min(m,n) and find the common factors that way -- it is much too slow!]
According to Euclid, the greatest common divisor, or gcd, can be found like so:
gcd(x,y) == gcd(y, x%y)
We can use that to quickly find gcd's. For example:
gcd(270,250) == gcd(250, 20) # 270 % 250 == 20
== gcd(20, 10) # 250 % 20 == 10
== gcd(10, 0) # 20 % 10 == 0
When we get to gcd(x,0), the answer is x. So gcd(270, 250) is 10. With this in mind, write the function gcd(x,y) that takes two positive integers x and y and returns their gcd using Euclid's gcd algorithm. - hasConsecutiveDigits(n) [2 pts]
Write the function hasConsecutiveDigits(n) that takes a possibly- negative int value n and returns True if that number contains two consecutive digits that are the same, and False otherwise. - nthAdditivePrime(n) [2 pts]
Write the function nthAdditivePrime(n) that takes a non-negative int n and returns the nth Additive Prime, which is a prime number such that the sum of its digits is also prime. For example, 113 is prime and 1+1+3==5 and 5 is also prime, so 113 is an Additive Prime. - mostFrequentDigit(n) [4 pts]
Write the function mostFrequentDigit(n), that takes a possibly-negative integer n and returns the digit from 0 to 9 that occurs most frequently in it, with ties going to the smaller digit. - isRotation(x, y) [4 pts]
Write the function isRotation(x, y) that takes two non-negative integers x and y, both guaranteed to not contain any 0's, and returns True if x is a rotation of the digits of y and False otherwise. For example, 3412 is a rotation of 1234. Any number is a rotation of itself. - integral(f, a, b, N) [4 pts]
Background: in calculus, we use the integral of a function f from x=a to x=b to compute the area under the curve between those points (or the negative area if the function is below the x-axis). One way to approximate this area (that is, to find it without doing any actual calculus!) is by replacing the smooth function with a collection of N trapezoids, as shown in this image (from here, with N=5):
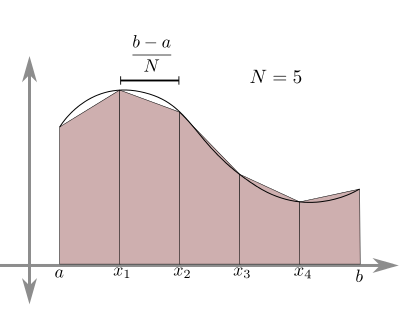
As in that image, here we will only use uniform widths, so each of the trapezoids has a width of (b - a)/N, so that all N of them together span the width of (b - a).
In any case, the larger N is, the more trapezoids you use, the more accurate your approximation becomes. You can read more here about this so-called trapezoidal rule.
With this in mind, write the function integral(f, a, b, N) that takes a Python function f (that itself takes one value x, a float, and returns a float), and two floats a and b, where a<=b, and a positive int N, and uses the trapezoidal rule with N trapezoids to return the approximate area under the curve of f(x) where a <= x <= b. To be clear, in the case where N=1, this uses just one trapezoid, where the left edge is at (a, f(a)) and the right edge is at (b, f(b)), so the result is (b - a) * (f(a) + f(b))/2 (the width times the average height of the trapezoid).
Hint: you should use almostEqual if you have your own tests or add any to our test function. Also, you'll probably want to use some very simple curves for testing, as we did in the test function, such as f(x)=x, f(x)=2*x+3, and f(x)=2*x**2, and then in ranges (a,b) with values of N such that you can fairly easily compute the expected answer by hand.
Another hint: here is a basic example showing how functions work as parameters to other functions:def f1(x): return x+1 def f2(x): return x+2 def h(f): return f(10) print(h(f1)) # calls f1(10), prints 11 print(h(f2)) # calls f2(10), prints 12
Part B [80 pts]
- Friday Lab [10 pts]
Attend your Friday lab (in your assigned recitation time). To receive full credit, you must show up on time, stay the whole time, be focused and uni-tasking (not multi-tasking), and fully participating. Note that if you received the Early Bird Bonus, you are excused from attending Friday lab, though you are still most welcome to attend. - findZeroWithBisection(f, x0, x1, epsilon) [15 pts]
Write the function findZeroWithBisection(f, x0, x1, epsilon) as described here. - carrylessAdd(x, y) [15 pts]
First, you may wish to read the first page (page 44) from here about Carryless Arithmetic. Or, just understand that carryless addition is what it sounds like -- regular addition, only with the carry from each column ignored. So, for example, if we carryless-ly add 8+7, we get 5 (ignore the carry). And if we add 18+27, we get 35 (still ignore the carry). With this in mind, write the function carrylessAdd(x, y) that takes two non-negative integers x and y and returns their carryless sum. As the paper demonstrates, carrylessAdd(785, 376) returns 51. - nthSmithNumber(n) [20 pts]
Write the function nthSmithNumber that takes a non-negative int n and returns the nth Smith number, where a Smith number is a composite (non-prime) the sum of whose digits are the sum of the digits of its prime factors (excluding 1). Note that if a prime number divides the Smith number multiple times, its digit sum is counted that many times. For example, 4 equals 2**2, so the prime factor 2 is counted twice, thus making 4 a Smith Number. - playPig() [20 pts] [manually graded]
Note: for only this problem, you may use strings but only in these ways:- Obtain a string from input().
- Check if two strings are equal.
- Print a string (including f-strings).
- Your game must enforce the basic rules of Pig.
- Your game should not use any graphics. This is a console-based game.
- Your game should use the input(prompt) function to get user input.
- Your game should print enough information to make the game reasonably fun and usable.
- Bonus/Optional: bonusPlay112 (The 112 Game) [1.5 pts]
Read the writeup for "The 112 Game" here (skip to Part B). Be sure to follow the spec exactly, so the autograder can properly grade your work! As with all bonus, we recommend that you only do this for the joy of learning (which is great), and not for the points (which are modest). - Bonus/Optional: bonusCarrylessMultiply(x, y) [1.5 pts]
Write the function bonusCarrylessMultiply(x, y), that works similarly to carrylessAdd(x, y) (which we will cover in the writing session), based on this paper on Carryless Arithmetic. This paper shows that bonusCarrylessMultiply(643, 59) returns 417. Hint: it may help if you do this differently than usual long multiplication. Instead of working by rows in the output, work by columns. So first compute all the ones digit values, and sum those mod 10. Then compute all the tens digit values, and sum those mod 10. And so on. You may assume x and y are non-negative.
Hint #1: do not solve carrylessMultiply(x, y) by simply calling carrylessAdd(x, result) a total of y times. That is wrong on two levels. First, it is simply too inefficient (what if we are multiplying 20-digit numbers?). Second, it is also wrong algorithmically! CarrylessMultiply is not like normal multiply, and if we take + to be carrylessAdd and * to be carrylessMultiply, then it is not necessarily true that (x * y) is the same as (x + x + ... + x + x) for a total of y x's. Yikes. So: stick with the next hint (see below). It also uses carrylessAdd and is fairly straightforward, but it is reasonable efficient and algorithmically correct. Good luck with it.
Hint #2: Here's a hint on one way to solve this problem (there are many ways, and this way is not the most efficient, to be sure, but it is efficient enough and it is perhaps among the clearest and easiest ways).
Consider multiplying 123 * 456. Observe that:
123 * 456 = 123 * 4 * 100 + 123 * 5 * 10 + 123 * 6
in this way, we actually only have to multiply 123 times a single digit each time, then multiply that result by the right power of 10. Right?
Ok, so now, to multiply by a single digit, we can instead just add that many times. That is:
123 * 6 == 123 + 123 + 123 + 123 + 123 + 123
Why is that interesting? Because we already have carrylessAdd, so we can just use that to do all this addition.
Of course, multiplying by simply adding is very inefficient. But since we are only doing it for multiplying by a single digit, there's a max of 9 additions (8 if you think about it), and so it's not so inefficient. It's actually acceptable, if not ideal, and certainly good enough for hw2, though again better approaches do exist.
Hope this helps. And, again, you can safely ignore all of this and solve this problem any way you wish. - Bonus/Optional: Integer Data Structures [2 pts]
Note: this is a fascinating but also very spicy bonus problem that will require substantial effort for minimal points. Only attempt this for the love of learning, and only if you truly have the time for it. See the Integer Data Structures writeup for details.