15-110 Spring 2011 Homework 3
Due Sunday, 6-Feb, at 6pm

Special Note:  Due to the Super Bowl, this week's hw is due Sunday at 6pm.  Also, we will provide extra coverage during the Sunday office hours prior to 6pm.  Go Steelers!!!!


Same basic directions as hw2, so read those carefully (replacing "hw2" with "hw3", where appropriate, of course).

Additional notes:


Practice:

  1. SOLO Problem-Solving (with Conditionals and Loops)  [35 pts]
    1. SOLO DNA Complementary Strands Verification [10 pts]
      Background: DNA strands are composed of sequences of 4 nucleotides (Adenine, Cytosine, Guanine, and Thymine).  Adenine and Thymine form A-T bond pairs, and Guanine and Cytosine form G-C bond pairs.  Two DNA strands are complementary, and so can form a double helix, if each corresponding nucleotide can form a bond pair.  For example, each Adenine in one strand must correspond to a Thymine in the other.

      Your task: Write the function areComplementaryStrands (in the file hw3-solo.py).  This function takes two DNA strands, represented as Python strings of the letters "A", "C", "G", and "T" (for the 4 nucleotides), and returns True if the two strands are complementary and False otherwise.         Here are some test cases for you:

          assert(areComplementaryStrands("AAGCATCA", "TTCGTAGT") == True)
          assert(areComplementaryStrands("AAG", "TTC") == True)
          assert(areComplementaryStrands("AAG", "TTT") == False)
          assert(areComplementaryStrands("AAG", "TTCC") == False)
    2. SOLO  Hardy-Weinberg Principle + Mendelian Genetics [10 pts]
      Background:  Read the wikipedia page on the Hardy-Weinberg Principle.  Note: this is not a course in genetics, so you really do not have to understand the Hardy-Weinberg Principle, nor is it a course in statistics, so you do not have to understand a chi-square test.  But you do have to understand how to take a page of fairly clear text describing straightforward algorithms and to translate them into working Python code!

      Your tasks:  First:  Write the function hardyWeinbergChiSquared       (in the file hw3-solo.py).  This function takes three values -- the observed populations with dominant (AA), heterozygous (Aa), and recessive (aa) genes -- and returns the value of chi-squared resulting from testing the "null hypothesis" that these values are in Hardy-Weinberg Frequencies.  Again, you do not have to really understand what that means to do this problem (though it would be nice, it's not required) -- you just have to follow the logic in the "Example chi-squared test for deviation" section of the article).  For example, that page includes a table of observed populations of Scarlet Tiger moths:
         Genotype:  White-spotted(AA)  Intermediate(Aa)  Little spotting(aa)
         Number:          1469               138                 5
      Following this table, the article provides a fully worked-out example showing how to derive the chi-squared value for this data. Note that in this section, obs(Q) means the observed number with property Q, and exp(Q) means the expected number with property Q (the closer these two are, the better the model fits the data).  For this data, chi-squared = 0.83, and so:
           hardyWeinbergChiSquared(1469, 138, 5)
      should return:
           0.83
      Hint:  this function may take integers as parameters -- beware of inadvertent errors caused by integer division!  In any case, here is a test case for you (the one given above, but coded in Python):

          assert(almostEqual(hardyWeinbergChiSquared(1469, 138, 5), 0.83))

      Note that this uses our almostEqual function because we cannot safely compare floating-point numbers for equality using "==" (why not?).  Here is our almostEqual function:

      def almostEqual(d1, d2):
          return abs(d1 - d2) < 0.001  # adjust this value as appropriate

      Second:  Write the function inHardyWeinbergFrequencies       (in the file hw3-solo.py).  This function takes three values -- the observed populations with dominant (AA), heterozygous (Aa), and recessive (aa) genes -- and returns True if these numbers are consistent with Hardy-Weinberg Frequencies  and False otherwise.  From the article, we see that this is true if the chi-squared test is below the 5% significance level, which for 1-degree of freedom (as we have here) is True if chi-squared is less than 3.84.  Thus, this function can be written in one line of code, using hardyWeinbergChiSquared as a helper function.  In the given example, chi-squared is 0.83, so your function would return True.  What does this True mean?  It means that, absent excessive forces from inbreeding, selection, mutation, or other "deviations", the observed ratios of Scarlet Tiger moths should be self-perpetuating. Fascinating!  Here is a test case for you (the one given above, but coded in Python):

          assert(inHardyWeinbergFrequencies(1469, 138, 5) == True)
    3. SOLO  Hardcoded 4-Person Knights and Knaves [10 pts]
      Background:  for this problem, we revisit Knights and Knaves.  Our goal is to write a general-purpose solver for any N-person Knights and Knaves problem.  For that, we need to use some techniques we've not yet covered.  So instead, this week we'll take a step in that direction, and write a solver for a specific 4-person problem       (though these techniques can be used to solve any specific Knights and Knaves problem).  We will solve Puzzle #145:
           Abe tells you, `I know that I am a knight and that Dave is a knave.'
           Dave claims, `Abe and I are the same.'
           Sally says that neither Abe nor Dave are knaves.
           Zippy claims that Abe is a knave.

      Note that you will receive zero credit if you manually solve the problem and then hardcode the answer.  To receive credit, you must follow the algorithm described here, in which your code closely follows the solution strategy we covered in the course notes on Knights and Knaves.

      Your tasks:  First, write the helper function psColumn4       (in the file hw3-solo.py) that takes 8 boolean (true/false) parameters:  the truth values for each of the four inhabitants (and here we are hardcoding for 4 inhabitants -- that's the 4 in psColumn4) -- call these A, B, C, and D for this explanation -- followed by the truth values of their statements (SA, SB, SC, SD).  Notice that this corresponds to one row of our truth table.  The function completes the truth table for that row, computing IA, IB, IC, and ID, and finally computing PS.  The function returns the value of PS for that row.   Here are some test cases for you:

          A = True
          B = True
          C = False
          D = False
          SA = True
          SB = True
          SC = False
          SD = False
          assert(psColumn4(A, B, C, D, SA, SB, SC, SD) == True)
          SD = True
          assert(psColumn4(A, B, C, D, SA, SB, SC, SD) == False) # because D != SD

      (Note:  when we assign required helper functions such as psColumn4, we will grade these -- robotically and/or manually -- as well as the main function in the exercise.)

      Second, write the function solveKnightsAndKnaves145       (in the file hw3-solo.py). This function takes no parameters and returns a string encoding the solution to the puzzle, where the participants are listed in alphabetic order, and uppercase means Knight and lowercase means Knave.  So, for example, "AdsZ" means that Abe and Zippy are knights, and Dave and Sally are knaves.  How do we write this function?  Simple:  we just call psColumn4 over and over again, once for each row -- if that function returns True, then we found the winning row, so we can return a string representing the truth values of the inhabitants on that row.  And to call psColumn4 once for each row, the function will use FOUR NESTED "for" LOOPS, with each loop assigning a value from 0 to 1, inclusively, to a variable representing one of the inhabitants.  Inside the innermost loop, assign truth values to A, D, S, and Z based on those 0-or-1 values in the loop variables, then assign values to SA, SD, SS, and SZ based on the problem statement, and finally call psColumn4 to finish the row.   Note that test cases are not really interesting here, since this function takes no inputs and always returns the same value; even so, here is the one-and-only test case for you:

          assert(solveKnightsAndKnaves145() == "Adsz")

      Yes, this includes the final answer to the problem (Abe is a knight, the rest are knaves).  You will be graded here not on what answer your function returns, but how it computes that answer.
  2. Collaborative Problem-Solving (with Conditionals and Loops)  [45 pts]
    1. DNA Strand Pattern Matching [10 pts]
      Background: Many questions in genetics involve searching for various patterns in DNA sequences.  Some of these searches require advanced algorithms, but others can be implemented with simpler algorithms.  Here we will explore a fairly straightforward DNA string pattern matcher.

      Your task:  Using the helper functions described below (so finish reading this entire question before starting!), write the function findPattern       (in the file hw3-collab.py) that takes two strings and an integer, where the first string represents a DNA sequence (composed of the symbols "A", "C", "G", and "T"), the second string represents a pattern to find, and the integer is the index in the DNA sequence from which to start the search.  The pattern is also composed of "A", "C", "G", and "T", but can also contain these characters:
         character  meaning
           "."      match any single letter ("A", "C", "G", or "T")
           "x"      match either "A" or "T"
           "y"      match either "C" or "G"
      Your function should return the index of the start of the first match (starting from the given start index), or -1 if there are no matches.   Here are some test cases for you:

                 assert(findPattern("CGACGATACGTTCT", "ACG", 0) == 2)
          assert(findPattern("CGACGATACGTTCT", "ACG", 3) == 7)
          assert(findPattern("CGACGATACGTTCT", "Cyx.C", 0) == 8)

      To encourage you to use functional composition, your findPattern function must use the helper function findPatternAtIndex.  This helper function takes three parameters -- the DNA string, the pattern string, and a specific targetIndex -- and returns True if the given pattern occurs in the given DNA string starting only at that given index, and False otherwise.  Your findPattern function will call this helper function repeatedly (presumably with different starting indexes).        Here are some test cases for you:

          assert(findPatternAtIndex("CGACGATACGTTCTC", "ACG", 0) == False)
          assert(findPatternAtIndex("CGACGATACGTTCTC", "ACG", 2) == True)
          assert(findPatternAtIndex("CGACGATACGTTCTC", "ACG", 7) == True)
          assert(findPatternAtIndex("CGACGATACGTTCTC", "Cyx.C", 0) == False)
          assert(findPatternAtIndex("CGACGATACGTTCTC", "Cyx.C", 3) == False)
          assert(findPatternAtIndex("CGACGATACGTTCTC", "Cyx.C", 8) == True)
          assert(findPatternAtIndex("CGACGATACGTTCTC", "Cyx.C", 14) == False)

      Continuing with the theme of functional composition, your findPatternAtIndex function must use the helper function symbolsMatch.  This function takes two symbols, one from a DNA string and one from a pattern string, and returns True if the two match as described above, and False otherwise.  Here are some test cases for you:

          assert(symbolsMatch("A", "A") == True)
          assert(symbolsMatch("A", "C") == False)
          assert(symbolsMatch("A", "x") == True)
          assert(symbolsMatch("T", "x") == True)
          assert(symbolsMatch("A", "y") == False)
          assert(symbolsMatch("T", "y") == False)
          assert(symbolsMatch("A", ".") == True)
          assert(symbolsMatch("C", ".") == True)
          assert(symbolsMatch("C", "y") == True)
          assert(symbolsMatch("G", "y") == True)
    2. Pendulum Motion  [10 pts]
      So you know:  In this problem you will be translating some complicated math into Python.  But don't fret!  This is not a math course, and you do not have to understand the underlying math (for the most part).  But you do have to understand how to translate it into Python.  This is an invaluable skill:  in many application areas, you will come across really complicated math expressions, the kind that are devilishly hard to reason over.  But if you can manage to code them into Python functions, then you can gain control over them and reason over them by running experiments on those Python functions.  What's more, even if the math itself is complicated, translating it into Python doesn't have to be.  That is a key point of this exercise.

      Background:  in high school physics, you may have learned that the period of a pendulum is the time it takes for the pendulum to swing all the way from one side to the other and back again.  What's more, this period is basically constant for a pendulum of a given length, which is what makes pendulum clocks work so well.  Specifically, high school classes usually teach that a pendulum of length L (in meters) has the following period (T, in seconds):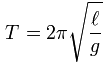
      Pendulum Simple Period
      Here, g is the force of gravity on Earth, or about 9.8 m/s2.  This not-so-complicated formula is a simplification that assumes that the period is independent of the initial angle at which you start the pendulum.  This assumption is false, as it turns out.  But for small angles, it works well enough, and it keeps the math much simpler, which is why the formula is usually taught like that in high school.

      Now, we'll use the "real" formula that depends both on L, the length of the pendulum (in meters), and theta0, the initial angle (in radians, where 0 radians is pointing downwards to start (so the pendulum doesn't move!), and pi/2 radians is holding the pendulum horizontally to start):

      Ok, now the math isn't so easy.  But, unfortunately, this time the math is real.  This is how pendulums really work.  So we need to reason over this math.  But how?  It's so complicated!  Answer:  code it up in a Python function, then use that function to reason over the math.  This may still be a little challenging, but it's definitely more doable for many people than directly analyzing the math.

      Your task:  Using the helper functions described below (so finish reading this entire question before starting!), write the function T(L, theta0) (in the file hw3-collab.py), which takes a length L in meters and an initial angle theta0 in radians, and returns the period T of the given pendulum according to the complicated formula above.  Then, answer the free-response questions at the end of this exercise.

      To solve this, we'll work the problem from the inside out.  Way on the inside we see n! and also (2n)!, where ! means factorial.  So we'll start here.  Write the function factorial that takes a non-negative integer n and returns n!, which is the product 1*2*...*n (or just 1 if n=0).         Here are some test cases for you:

          assert(factorial(1) == 1)
          assert(factorial(5) == 5*4*3*2*1)
          assert(factorial(10) == 10*9*8*7*6*5*4*3*2*1)
          assert(factorial(0) == 1)

      Next, we'll take on the part of the equation inside the big brackets:

      This expression uses two variables, n and theta0, so we'll model it as a Python function seriesTerm (the name should become clear soon), that takes two parameters, n and theta0.  Naturally, this function will use the factorial function we just wrote.  It will also have to use the function math.sin to compute the sine function (and for that you will have to "import math").  It will also have to use the ** operator for exponentiation. Also, note that sin2n(x) means the same thing as (sin(x))2n.  Armed with this information, write the function seriesTerm(n, theta0).  The file hw3-collab.py includes a few test cases for you, and while they are helpful for testing purposes, they are not very illustrative, so we omit them here.

      At this point, we can replace the expression in the brackets with the function seriesTerm(n, theta0), so we have:

      Next, we need to take on the sigma (the angular S-like (or perhaps E-like) symbol with the n=0 below and the infinity sign above). This sigma indicates that we should add up all the values of seriesTerm(n, theta0) where n goes from 0 to infinity.  Now, it's hard to add an infinite number of terms in Python, so we'll just go up to n=k (inclusively), for some finite k.  So we have:
           seriesSum(k, theta0) = seriesTerm(0,theta0) + seriesTerm(1,theta0) + ... + seriesTerm(k,theta0)
      Now this doesn't look so bad!  Write the function seriesSum that takes an integer k (the largest value of n in the series) and       the angle theta0, and returns the sum given above.  As before, a test function is included in the file hw3-collab.py for this function.

      So now we have:

      And now you can take this all the way home.  Write the function T(L,theta0) that computes the previous expression (use math.pi for the value of pi).  Note that we need to choose a value for k -- how many terms to use from the seriesSum.  For now, let's go with k=20.   Again, a (modest) test function is included for this function.

      And there you have it!  You have modeled that complicated math expression as a Python function.  Congratulations!  And so now we ask a few questions about that function.  Include your answers in the file hw3.doc (or whatever legal extension you prefer), which should be placed in the hw3.zip file you submit.  For each question, provide both an answer to the question and a clear explanation as to how you used the T(L,theta0) Python function to answer the question.
      1. First, confirm that the simple formula (the one that does not depend on the starting angle theta0) and our more complicated formula, T(L,theta0), return the same value when theta0 is 0, regardless of the length L.  Try a few different L's to confirm. Be sure to use almostEqual and not == in your test, since we are dealing with floating-point numbers here, so some small error is acceptable and expected.
      2. Looking at the formula for T, it appears that as theta0 increases, T increases.  That is, as our starting angle increases, the actual period is longer than the period predicted by the simple formula.  For a 1-meter pendulum, how many times longer is the actual period than the period predicted by the simple formula when theta0 is 5 degrees (which equals pi/36 radians)?  (That is, what is the ratio of T(1,pi/36) to SF(1), where SF is the simple formula that only depends on L and not theta0?)
      3. Repeat the previous question where theta0 is 90 degrees (which equals pi/2 radians, or when we start with the pendulum extended horizontally).
      4. Repeat the previous question using a length L of 100 meters. Does the result depend on the length of the pendulum?
      5. Do you think the predicted error in the simple formula is large enough that you could observe it in a real, physical pendulum? Why or why not?  In any case, what starting angle between 0 and 90 degrees appears to give the best chance of observing the predicted error?
      6. We somewhat arbitrarily chose a value of 20 for k.  Try different values for k (the number of terms we used when computing the seriesSum), then suggest if 20 is a good value to use, or if you think there is a better value to use. Either way, briefly explain your answer.  Why not use a value of, say, 1 million to ensure super-high accuracy?
      7. Bonus/Optional (1 pt):  Use your Python function to determine the angle at which the observed period will be 2% longer than the time predicted by the simple formula.  Hint:  you can use binary search for this.  You know that a theta0 of 0 is too low, and as a hint, a theta0 of pi/2 is too high (though you should verify this).  So keep dividing in half until you get fairly close to the answer (remember not to use == with floating-point numbers).
      8. Bonus/Optional (2 pts):  Construct an actual physical pendulum (we used some string and a light weight for ours).  For credit, submit a jpg picture (no larger than 50k) in your hw3.zip file of you with your pendulum.  Next, do the physical experiments necessary to try to confirm what your Python models predict.  That is, start your pendulum at some small angle and measure its period.  Does the simple formula predict the behavior?  How about the more complicated formula?  Then increase the theta0 to, say, 90 degrees (pi/2 radians, or starting at the horizontal), and answer those same questions.
    3. Blackjack  [10 pts]
      Note:  We'll wrap up this week with something a bit more lighthearted, but still important.  Not only does blackjack stress loops and conditionals along with problem-solving (our topics of the week), but it's a complete (if simple) program.   While most of what we write in this stage of the course are standalone functions, we should be moving towards writing entire applications that are reasonably usable.  This is our first one.  Have fun!

      Background:  Here we will write a simplified version of Blackjack, without most of the complexities (betting, splitting, doubling down, and so on).  In our simple version, we start each round with a new shuffled deck.  The dealer (the computer) is dealt one card and the player (the human) is dealt two cards.  The player can see all cards dealt.  The score of a hand (dealer's or player's) is the sum of the face values of the cards, where aces count as 1, except an ace counts as 11 if this would not make the hand "bust" (exceed 21). The round proceeds with the player repeatedly facing the choice of "hitting" (taking a card) or "standing" (ending this part of the round).  If the player "busts" (scores over 21), the dealer wins the round.  Otherwise, once the player stands, the dealer starts taking cards until either the dealer scores 17 or higher, or the dealer "busts" (scores over 21, in which case the player wins the round).  If neither party busts and the round ends, then the hand with the higher score wins the round, with ties decided in the dealer's favor.

      As for implementing blackjack, seeing as we have not yet covered lists, we have modeled a deck of cards using a single string of hyphen-separated cards, like so:
      3H-4D-AH-7D-TH-KH-KC-QD-8S-QH-QC-4H-6H-9H-9C-7H-AS-8H-TD-6C-7S-4S-2S-TS-JH-5C-JD-8C-TC-6D-2H-AC-AD-2C-3D-3S-JS-JC-7C-3C-9D-QS-9S-KS-4C-5D-8D-6S-2D-5S-5H-KD
      We have also provided you with the function getRandomDeck that takes no parameters and returns a new shuffled deck each time you call it.  You are not responsible for how the getRandomDeck function works, but you should understand how to use it.

      In fact, we have provided more than that for this problem.  We have written most of the game already!  Your task is to finish the writing the game, adding two key functions missing from our implementation.

      Your task:  First, write the function blackjackScore (in the file hw3-collab.py).  This function takes a hand of cards (represented as a string, just like the deck), and returns the score of those cards in blackjack.  As noted above, the score is the sum of the face values of the cards, but with special treatment for aces (which are 1 unless they can be 11 without busting).  Here are some test cases for you:

          assert(blackjackScore("2H") == 2)
          assert(blackjackScore("TD") == 10)
          assert(blackjackScore("QC") == 10)
          assert(blackjackScore("AS") == 11)
          assert(blackjackScore("2H-5C-TD-4S") == 21)
          assert(blackjackScore("2H-5C-TD-4S-2C") == 23) # bust!
          assert(blackjackScore("JS-KD-AC") == 21)
          assert(blackjackScore("9S-AC") == 20)
          assert(blackjackScore("9S-AC-AD") == 21)
          assert(blackjackScore("9S-AC-AD-AS") == 12)

      Next, study the function playBlackjackRound that we have provided for you (and which uses the blackjackScore function that you just wrote!).  You should understand this function thoroughly for quiz3.  For now, though, you mainly need to understand its high-level behavior:  it plays one full round of blackjack, and returns True if the player (the human) wins and False otherwise (if the computer dealer wins).  There is nothing to submit for this step, just study the code for a while.

      Next, write the function playBlackjack.  This function takes no parameters and returns nothing, but it's far from useless!  It plays a game of blackjack by repeatedly calling the playBlackjackRound function that we have given you.  It also keeps track of the wins and losses, and asks the user whether to keep playing or not.  To specify the behavior of this function, we will provide a transcript of an actual game.  Make your function match the behavior of this transcript (though, of course, the actual cards and player decisions will vary each time you play):

      --------------------------------
      Welcome to blackjack!
      --------------------------------
      Your turn...
      Dealer is showing: AS
      Your hand: 3H-8D
      Your score: 11
      Hit or Stand?  h
      Dealer is showing: AS
      Your hand: 3H-8D-9D
      Your score: 20
      Hit or Stand?  s
      Now it's my turn...
      Dealer draws: AD   (press Enter to continue)
         Dealer hand:   AS-AD
         Dealer score:  12
         Player score:  20
      Dealer draws: 5S   (press Enter to continue)
         Dealer hand:   AS-AD-5S
         Dealer score:  17
         Player score:  20
      You won this round!
      Play again?   y
      --------------------------------
      Player rounds won:   1
      Dealer rounds won:   0
      Your turn...
      Dealer is showing: 6S
      Your hand: AD-5C
      Your score: 16
      Hit or Stand?  h
      Dealer is showing: 6S
      Your hand: AD-5C-4H
      Your score: 20
      Hit or Stand?  h
      Dealer is showing: 6S
      Your hand: AD-5C-4H-2H
      Your score: 12
      Hit or Stand?  h
      Dealer is showing: 6S
      Your hand: AD-5C-4H-2H-3S
      Your score: 15
      Hit or Stand?  h
      Dealer is showing: 6S
      Your hand: AD-5C-4H-2H-3S-8S
      Your score: 23
      You bust! (your score is over 21)
      Play again?   y
      --------------------------------
      Player rounds won:   1
      Dealer rounds won:   1
      Your turn...
      Dealer is showing: 4D
      Your hand: KD-5D
      Your score: 15
      Hit or Stand?  s
      Now it's my turn...
      Dealer draws: 7C   (press Enter to continue)
         Dealer hand:   4D-7C
         Dealer score:  11
         Player score:  15
      Dealer draws: KS   (press Enter to continue)
         Dealer hand:   4D-7C-KS
         Dealer score:  21
         Player score:  15
      I have a higher score.  I win this round!
      Play again?   n
      Goodbye!
  3. Readings in Computational Thinking  [20 pts]
    1. Watson  [10 pts]
      Watch this short video on Watson, the impressive Jeopardy-playing program written by IBM (in collaboration with CMU!) that has been garnering much press of late.   At the end of the video, there is a reference to how this is not just about game-playing, but how it could revolutionize certain aspects of business.  Briefly reflect on this point.   Is this a game-changer?  Will this radically change your life (maybe not when it is playing Jeopardy, but when it is applied in other ways)?  If so, how (and if not, why not)?  And even if it won't be a radical game-changer, will it be a money-maker?  That is, will it make some business processes (whether for consumers or not) sufficiently more efficient to justify the expense of this approach?  Speculate, but explain your reasoning.
    2. Human Genome Sequencing and String Matching  [10 pts]
      Watch this short video on human genome sequencing.  Briefly explain how string matching, like we did in this hw (only with a bit more sophistication), played a critical role in sequencing the human genome.
  4. Bonus/Optional:  Week #3 Bonus/Honors Topic   [5 pts]
    See the Hw3 bonus writeup.