First, take practice-quiz2 and also (perhaps in a separate sitting) quiz2 from s13, both under quiz conditions (working solo, without a computer, with only 20 minutes, etc). Then, using a computer as you wish (and CA's, office hours, etc, but still under the "solo" rules), write a solution set to each, placing those solutions in a triple-quoted string at the top of hw2.py that you submit.
Note: a triple-quoted string looks like this:
"""
You can place anything here (up until the next triple-quote)
and Python will essentially ignore it.
"""
Background: read the first paragraph from the Wikipedia page on happy numbers. After some thought, we see that no matter what number we start with, when we keep replacing the number by the sum of the squares of its digits, we'll always either arrive at 4 (unhappy) or at 1 (happy). With that in mind, we want to write the function nthHappyNumber(n). However, to write that function, we'll first need to write isHappyNumber(n) (right?). And to right that function, we'll first need to write sumOfSquaresOfDigits(n). And that's top-down design! Here we go....
-
sumOfSquaresOfDigits(n)
Write the function sumOfSquaresOfDigits(n) which takes a non-negative integer and returns the sum of the squares of its digits. Here are some test assertions for you:
assert(sumOfSquaresOfDigits(5) == 25) # 5**2 = 25
assert(sumOfSquaresOfDigits(12) == 5) # 1**2 + 2**2 = 1+4 = 5
assert(sumOfSquaresOfDigits(234) == 29) # 2**2 + 3**2 + 4**2 = 4 + 9 + 16 = 29
print "Passed all tests!" - isHappyNumber(n)
Write the function isHappyNumber(n) which takes a possibly-negative integer and returns True if it is happy and False otherwise. Note that all numbers less than 1 are not happy. Here are some test assertions for you:
assert(isHappyNumber(-7) == False)
assert(isHappyNumber(1) == True)
assert(isHappyNumber(2) == False)
assert(isHappyNumber(97) == True)
assert(isHappyNumber(98) == False)
assert(isHappyNumber(404) == True)
assert(isHappyNumber(405) == False)
print "Passed all tests!" - nthHappyNumber(n)
Write the function nthHappyNumber(n) which takes a non-negative integer and returns the nth happy number (where the 0th happy number is 1). Here are some test assertions for you:
assert(nthHappyNumber(0) == 1)
assert(nthHappyNumber(1) == 7)
assert(nthHappyNumber(2) == 10)
assert(nthHappyNumber(3) == 13)
assert(nthHappyNumber(4) == 19)
assert(nthHappyNumber(5) == 23)
assert(nthHappyNumber(6) == 28)
assert(nthHappyNumber(7) == 31)
print "Passed all tests!" - nthHappyPrime(n)
A happy prime is a number that is both happy and prime. Write the function nthHappyPrime(n) which takes a non-negative integer and returns the nth happy prime number (where the 0th happy prime number is 7).
In this exercise, we will observe an amazing property of the prime numbers!
- The Prime Counting Function: pi(n)
Write the function pi(n) (which has nothing much to do with the value "pi", but coincidentally shares its name) that takes an integer n and returns the number of prime numbers less than or equal to n. Here are some test assertions for you:
assert(pi(1) == 0)
assert(pi(2) == 1)
assert(pi(3) == 2)
assert(pi(4) == 2)
assert(pi(5) == 3)
assert(pi(100) == 25) # there are 25 primes in the range [2,100]
print "Passed all tests!"
- The Harmonic Number: h(n)
Write the function h(n) that takes an int n and, if n is positive, returns the sum of the first n terms in the harmonic series: 1/1 + 1/2 + 1/3 + 1/4 + ... If n is non-positive, the function returns 0. Here are some test assertions for you:
assert(almostEquals(h(0),0.0))
assert(almostEquals(h(1),1/1.0 )) # h(1) = 1/1
assert(almostEquals(h(2),1/1.0 + 1/2.0 )) # h(2) = 1/1 + 1/2
assert(almostEquals(h(3),1/1.0 + 1/2.0 + 1/3.0)) # h(3) = 1/1 + 1/2 + 1/3
print "Passed all tests!"
Note: here we use "almostEquals" rather than "==" because this function returns a floating-point number. You should also write almostEquals.
- Using the Harmonic Number to estimate the Prime Counting
Function (Wow!)
Write the function estimatedPi(n) that uses the Harmonic Number function to estimate the Prime Counting Function. Think about it. One counts the number of primes. The other adds the reciprocals of the integers. They seem totally unrelated, but they are in fact very deeply related! In any case, this function takes an integer n and if it is greater than 2, returns the value (n / (h(n) - 1.5) ), rounded to the nearest integer (and then cast to an int). If n is 2 or less, the function returns 0. Here are some test assertions for you:
assert(estimatedPi(100) == 27)
print "Passed all tests!"
- Empirical check that this really works:
estimatedPiError
Write the function estimatedPiError that takes an integer n and returns the absolute value of the difference between the value of our estimation computed by estimatedPi(n) and the actual number of primes less than or equal to n as computed by pi(n). If n is 2 or less, then function returns 0. Here is the start of a test function:
assert(estimatedPiError(100) == 2) # pi(100) = 25, estimatedPi(100) = 27
assert(estimatedPiError(200) == 0) # pi(200) = 46, estimatedPi(200) = 46
assert(estimatedPiError(300) == 1) # pi(300) = 62, estimatedPi(300) = 63
assert(estimatedPiError(400) == 1) # pi(400) = 78, estimatedPi(400) = 79
assert(estimatedPiError(500) == 1) # pi(500) = 95, estimatedPi(500) = 94
print "Passed all tests!"
Aside: as you can see, the estimatedPi function is an amazingly accurate estimation of the pi function. For example, the estimatedPi function predicts that there should be 94 prime numbers up to 500, and in fact there are 95 prime numbers in that range. And so we must conclude that there is some kind of very deep relationship between the sum of the reciprocals of the integers (1/1 + 1/2 + ...) and the number of prime numbers. This relationship has been explored in great detail by many mathematicians over the past few hundred years, with some of the most important results in modern mathematics relating to it.
We will say that a prime number p is "goofy" (obviously an invented term in this context) if p contains at least one even digit, and when all the even digits of p are removed, the resulting number is also prime. So, for example, 1429 is prime and when you remove all the even digits you get 19, which is also prime, so 1429 is a goofy prime. With this in mind, write the function nthGoofyPrime(n) which takes a non-negative integer n and returns the nth goofy prime. Note that the first goofy prime is 23, so nthGoofyPrime(0) returns 23.
Here you will draw this pattern (drawn twice, once in a 10x10 grid, and again in a 5x5 grid):

More precisely, write the function drawCirclePattern(canvas, x0, y0, x1, y1, rows) that takes a canvas, then four values that describe a rectangular region from (x0,y0) to (x1,y1), and finally the number of rows in the pattern (note that this is also the number of columns in the pattern). For example, the left image above was drawn with 10 rows (and 10 columns), and the right image with 5 rows (and 5 columns). The pattern consists of "buttons" (or perhaps "bullseyes"), where each button is really several circles drawn on top of each other. Each circle in a "button" has a radius 2/3rds as large as the next-larger circle, which continues until the radius is less than 1. As for the color of each button, here are the rules to follow:
Rule 1: Starting from the left-top corner, every 4th diagonal is entirely red.
Rule 2: For the non-red buttons, starting from the top row, every 3rd row is entirely green.
Rule 3: For the non-red and non-green buttons, starting from the second-to-leftmost column, every 2nd column is entirely yellow.
Rule 4: Any non-red, non-green, and non-yellow button is blue.
Note that these rules can be fairly easily implemented using a single if-elif-elif-else statement. Inside that statement, you might want to set a variable, say one named "color", based on each of these four conditions. Then you could draw with fill=color.
Note: You can assume that the width and height of the given rectangular region are both multiples of the numbers of rows and cols.
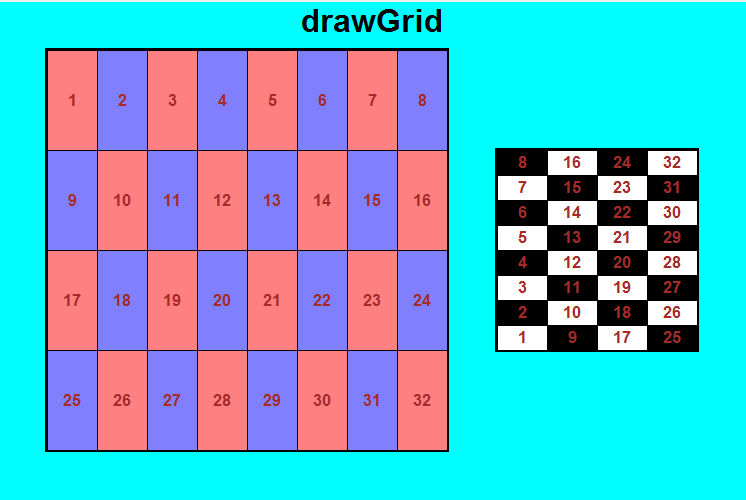
Write the function drawGrid that takes 5 values – a canvas, a left, top, right, and bottom – describing a rectangular region of the canvas, and fills this region with a drawing of a rectangular grid. For large areas (>200 pixels wide), the grid should have 4 rows and 8 columns, with cells alternating in the shades of red and blue in the image below (or fairly close to them in any case). For smaller areas, the grid should have 8 rows and 4 columns, and the cells should alternate black and white. Also, each cell will be labeled with a number (note that you can provide a number as the text value in create_text). For large areas, the numbers start in the left-top cell and proceed rightwards and then downwards. For small areas, the numbers start in the bottom-left cell and proceed upwards and then rightwards. Here is a screenshot to help:
Write the function drawSpiral that takes 5 values – a canvas, a left, top, right, and bottom – describing a rectangular region of the canvas, and fills this region with a drawing of an spiral (or really a series of spiral arms). The spiral arms must be created by drawing a series of circles (the only thing drawn in this exercise are small circles). There should be 28 arms, each arm composed of 32 circles. Each arm spirals, or bends, such that the outermost circle in the arm is drawn pi/4 radians (45 degrees) beyond the innermost circle in that same arm. Hint: You will have to use basic trigonometry here! Also, try to make the color gradients work as indicated. Here is a screenshot to help:

Hint: blue increases from 0 to 255 as the arm spirals outward. Green does the opposite. Only red's behavior changes based on the image size. For the smaller image, red increases from 0 to 128 (not 255). For the larger image, red does something else (what?).