These notes were prepared by
students attending this optional lecture. As such, they may contain a
small error here or there (standard disclaimer). They are provided here
as a service to those who may have missed the lecture.
How a Computer Works
In order to build a computer, we need a starting point. We could
use sand (which is made of silicon for its semi-conduction properties), but
instead we’re going to assume we already have logic gates and go through the
following steps:
1. Logic to circuits
2. Circuits to arithmetic
3. Memory
Logic to circuits
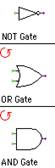
We are given different types of physical gates (AND, OR, NOT,
XOR) from which we want to first try to compute logical expressions. These
gates take two abstract values (True/False). Second, we want to count the total
possible number of boolean logical functions, and then
be sure we can compute any/all of them.
ØCan we build an XOR without an XOR gate?
Yes! We can use a NOT gate with the following expression: (x and
(not y)) or (y and (not x))

(You can simulate these gates here: http://math.hws.edu/TMCM/java/labs/xLogicCircuitsLab1.html)
If I have two variables that can each take on two values (0 and
1), there are 4 rows in the truth table. This equates to 2**4 possible
functions. How many unique functions would we have with three variables? We’d
have 8 rows in the truth table representation, so 2**8! And for 4 inputs, there are 2**(2**4), or 65,536 unique functions. We can’t possibly expect to build all these
different kinds of logic gates. Instead,
we need a way to construct any of these possible functions using just a small
set of physical logic gates.
Ø Is it possible to build something using a smaller amount of
gates?
Yes! First identify the rows whose outputs are 1s and then come
up with a function that’s True for only that row. So, to show an example of
breaking down the XOR…
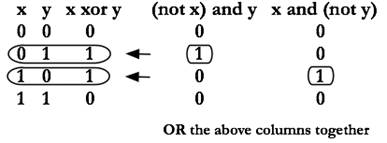
In this way, any boolean function can be represented with disjunctive normal form, meaning you can
do anything with AND, OR, and NOT gates.
ØIs it possible to get down
to using 2 gates?
Yes! We need to use DeMorgan’s Law.
![]()
In this way, we can replace every AND with a combination of OR
and NOT.
ØIs it possible to get down
to using only 1 gate?
No amount of OR-ing will build a NOT
gate (or vice-versa), but we could try a new direction: NOR! NOR-ing two values produces the same result as OR-ing them together and negating the output. Note that 0 NOR
0 = 1 and 1 NOR 1 = 0, and so x NOR x = NOT x.
So we can construct NOT using just NOR.
Also:
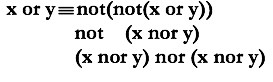
So we can also construct OR using just NOR.
Great!
So, the breakdown of simplification is as follows:
Everything -> Disjunctive Normal Form -> AND/OR/NOT -> DeMorgan’s -> OR/NOT -> NOR/OR (using x nor x trick)
-> NOR
This shows that we can physically compute any boolean
logic function with a collection of NOR gates. Naturally, the same is true with
NAND gates! Amazing!
Circuits to Arithmetic
To be a computer, we need to do arithmetic. We need to find a way
to represent the process of adding numbers with gates.
However, we don’t know how to represent numbers! Using numbers
violates our basic starting point because we were only given gates, wires,
batteries and switches. One solution:
represent numbers in binary where each digit is represented as a wire so
we can then take numbers and represent them in our framework.
Basic 1 bit addition
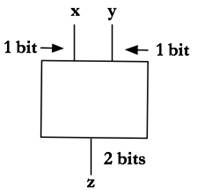
The fundamental difference here is that instead of having 2
output values, the function only has 1 output value so we treat each value as
its own function. This takes us from arithmetic to logic.
We represent this in a truth table and notice that the first
column is AND and the second column is XOR:
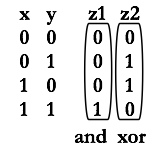
A half adder adds two 1-bit numbers and outputs one 2-bit
number. If we now add three 1-bit numbers, we can create a full adder! An
example of this would be if we were adding two binary numbers where the third
bit in each column would be the carry. This would still only need 2 bits for
output (since three is 11 in binary).
We can daisy chain adders like in this 4 bit adder example from
the website mentioned above. The smallest number with a 5th bit is
32, so the biggest number with 4 bits is 31. If we try 8+8, it goes to overflow
bit because it’s too big to represent.

Ø How do we build a 4 bit subtractor?
We use 2s complement! Check out the 4-bit minus diagram.
Memory Circuit
Now we need memory for our computer. The important concept of a
memory circuit is that the output feeds back into itself.
(http://math.hws.edu/TMCM/java/labs/xLogicCircuitsLab2.html)
How it works:
1.
Use the input on the left
to determine the value you want to store (to set the memory).
2.
Strobe (turn on/off) the
input at the top. This sets the memory
(the value on the right) to that value.
3.
The memory (the value on
the right) will stay constant until you repeat steps 1 and 2 above.
So, we can now store data and compute arithmetic over it!
ØHow do we move to a computer?
We’re going to use the Von
Neumann Architecture. This was realized in the Colossus machine in England
during WWII to crack codes, and in other machines at that time to compute
firing tables, support increasingly sophisticated radar, etc.
Look at the Intro to xComputer in the website mentioned earlier and click
launch. This is a simplified version of a computer (but not too simple – this
is basically what got us to the moon!).
· We can get to/from memory across a “bus” of wires between the
CPU and memory. For example, the bus could do the following:
o
Send a memory address (1s
and 0s)
o
Send a value to store at
that address
o
Send “store this please”
·
Data and programs are both stored
in memory. The operating system and hardware need to keep track of which is
which.
·
In a stored instruction,
the opcode (usually in the most significant bits)
specifies the operation to be performed. The constants that you need are in the
least significant bits.
·
PC (program counter) is an
address in memory that lets you know where you are in the program
·
AC (accumulator) is a value
stored in the CPU (as opposed to main memory) that lets you hold onto
intermediate steps
·
Fetch-decode-execute cycle:
o
Go to PC in memory, load
the value and put it into the instruction register
o
Increment the PC to point
to the next instruction.
o
Decode the instruction to
determine what action needs to take place
o
Perform computations with
the AC and store it back in memory
The sample assembly code we looked at in class modifies the program (thus blurring the
lines between program and data)! Increment the PC to walk through it and see
what it does!
Ultimately, we’ve taken logic/arithmetic and coupled it with
machines that allow us to perform computations and store back into memory.
ØArguing that this is all
you need
To reason over computational models (such as to prove the
Halting Problem), Alan Turing invented the Turing Machine, where all you have
is a single read-write tape of memory, a read/write head that is over one value
on that tape, a current state that you are in, and a table that indicates for
each combination of a state and a value under the read/write head, a value to
write, a direction to move the head, and a new state to move to. That’s it.
In order to see an example, look at the xTuringMachine lab in the provided website.
The Church Turing Thesis
basically states that anything that can be computed at all can be computed with a Turing machine. For today, a model of
computation is considered general purpose if it is Turing-equivalent, that is,
if you can use it to simulate an arbitrary Turing machine. And even our simple
machine model from above (or one quite a bit simpler), let alone Python or Java
or any modern programming language, is Turing-equivalent. And so:
nothing can be done with high level programming languages that can’t be
done with this simple computer. Computers
can get faster and more elegant, but
we can’t make them more powerful – we’ve reached the edge. At least until someone breaks through the
assumptions behind the Church Turing Thesis (for example, maybe by doing
infinite computation in a finite amount of time, now that would be a
game-changer!).